Table of Contents
computehrv
Motivation
Both heart beat onsets (R wave time points) as well as sliding beats-per-minute (BPM) are already interesting measures, but most publications refer to summary measures when GCR data reported. One of the most common of these is heart-rate variability (HRV). This function computes the power spectral contribution of frequencies in two specified ranges.
Requirements
To use this function, you must already have pre-processed the data and also detected the heart beats (for a complete example see below). The onset data must be given as either a list of onsets (R wave time points) or a one-dimensional vector representing time which is then used to detect the onsets.
Function reference ('help computehrv')
computehrv - compute HRV from onsets
FORMAT: hrv = computehrv(onsets [, opts])
Input fields:
onsets Ox1 or 1xO vector of onsets
opts optional settings
.detrend detrending of time series, either 'mean' or {'linear'}
.diffmeth either of 'betweenr' or {'onr'}
.filter filter size of resampled data in seconds (default: 0)
.findons boolean flag, onsets is a Tx1 vector (default: false)
.fftunits units for FFT output, either of {'squared'} or 'dB'
.freq sampling frequency of onset units (default: 1)
.hfreq higher HRV frequency range (default: [0.15, 0.4])
.lfreq higher HRV frequency range (default: [0.04, 0.15])
.method either of 'direct' or {'pwelch'}
.pwwin window size for pwelch in seconds (default: 100)
.relpow compute power as ratio over total power (default: true)
.resfreq resampling frequency in Hertz(default: 10)
.usefreq instead of computing the PSD over the RR wave form,
this computes over frequency in seconds (default: false)
Output fields:
hrv struct with fields
.detrend detrending selection used
.diffmeth diffmeth used, either 'b' (betweenr) or 'o' (onr)
.fftunits FFT units used, either 'd' (dB) or 's' (squared)
.findons flag whether the onsets were looked up
.freq given sampling frequency of onset data
.hfi indices of the high-frequency range into .praw
.hfp high-frequency power estimate (contribution)
.hfreq selected frequency range for high frequencies
.lfi indices of the low-frequency range into .praw
.lfp low-frequency power estimate (contribution)
.lfreq selected frequency range for low frequencies
.method FFT method used, either 'd' (direct) or 'p' (pwelch)
.onsets onsets (0-based, in 1Hz sampling)
.praw raw power spectrum (normalized FFT/pwelch output)
.prawf raw power spectrum frequencies (e.g. for plot)
.pwo pwelch options used (struct)
.pwwin pwelch window used (only relevant if .method == 'p')
.relpow flag whether .hfp/.lfp are relative to total power
.resfreq resampling frequency used
.rmssd RMSSD measure (alternative measure for variability)
.rri RRi plot data
.rrifreq inverse RRi (frequency) plot data
.totalp sum of power contribution (1 if .relpow == true)
.totalpr total raw power (amplitude)
.usefreq flag whether computation used .rrifreq rather than .rri
Arguments
onsets
The onsets can either be given as a Ox1 vector of numbers (the function sorts this vector, so order doesn't matter) or as a Tx1 vector representing the heart beat data. If this is the case, the .freq option must be set!
opts
detrend
The default for detrending the RRi-data is to remove both the mean and first-order polynomial (linear) fit of the signal. In case you wish to remove only the mean, you must set this flag to 'mean'. Please note that this does NOT influence the relation of the power contributions (.hfp / .lfp), and also does not (significantly) influence the raw scores of .lfp and .hfp, but naturally influences the relative contribution compared to the total power of all frequencies!
diffmeth
This flag has the following options:
'betweenr' - instead of computing the distance between R wave onsets (beats), the difference between the centers of onsets is computed, so that each beat can be assigned the average of the interval which precedes and follows it; for the beats at the border, the first derivative is kept constant'onr' (default) - this is the more common way of computing the distance between beats
Please note that this, in effect, imposes a rectangular (low-pass) filter over the raw onset data, which removes frequencies higher than 30/BPM, that is if the (average) BPM for a list of beats is 80, frequencies greater than 0.375Hz will be (more or less) removed! It is thus mostly useful for quality control of the signal (e.g. to see how much of the total power is contained in those very high frequencies).
findons
This flag forces the function to interpret the data as a Tx1 vector instead of an Ox1 list. The default is to determine this flag from the data: if the onsets data is a vector of few discreet values, this flag will be enabled, otherwise the data is interpreted as a list of onsets (time points).
fftunits
This flag has the following options:
'dB' - this applies a log-transform:10 * log10(FFT_SQUARED)'squared' (default) - this returns values computed asFFT_SQUARED = abs(FFT_RESULT) .^ 2
freq
For onset data, the default is to assume that onsets are given in seconds (1Hz). This can be changed (e.g. in case the onsets are in the sampling frequency of the original ECG data), and this flag must be set in case the given onsets are a Tx1 vector.
hfreq
High(er) frequency range for which a power contribution is computed (default: 0.15Hz to 0.4 Hz)
lfreq
Low(er) frequency range for which a power contribution is computed (default: 0.04Hz to 0.15Hz)
method
This flag has the following options:
'direct' - this sets the window to the entire signal, the FFT is computed by pwelch and returned'pwelch' (default) - this enables a sliding window-approach (for instance, compare basic FFT to Welch's method on wikipedia)
As an excerpt from wikipedia:
Welch's method is an improvement on the standard periodogram spectrum estimating method and Bartlett's method in that it reduces noise in the estimated power spectra in exchange for reducing the frequency resolution. Due to the noise caused by imperfect and finite data, the noise reduction from Welch's method is often desired.
Given that the signal is not circular in nature (there are potential problems with the discontinuity at the beginning and end of the signal), Welch's method is the default (at the expense of losing very low frequencies lower than 0.02Hz, given then default pwelch window size).
pwwin
This flag configures the window size when (and if) the pwelch function is used. The default is the greater value of 100 and 1 / (2 * opts.lfreq(1)) to ensure that no low frequencies of interest are dropped.
relpow
If set to true (the default), the power contribution values will be set in relation (ratio) to the sum of the power of all frequencies (relative contribution of power).
resfreq
This sets the re-sampling frequency which is applied when converting the raw RRi interval data to a continuous waveform (for further explanation see below).
usefreq
If set to true (default is false!), the FFT/Welch's method will not be computed over the RRi (raw) data but over the frequency-transformed data (which is not skewed as much, see below for more information); as I didn't find any reference to this transformation, this is (currently) not the default.
Algorithm
The algorithm of the function comprises the following (conditional) steps:
- if required, the Tx1 vector will be scanned for onsets (by computing the derivative over
TIMESERIES > MEAN(TIMESERIES)and locating those samples for which the time series switches from below mean to above mean (diff > 0); as a pre-caution, if any interval is less than 0.2 seconds (300BPM) or more than 3 seconds (20BPM), an error is raised - the onsets are sorted and the first value is subtracted from the other values
- if necessary, the onsets are converted to 1Hz temporal resolution
- given the chosen method to compute the BPMs (
onrvs.betweenr), the raw RRi time series is derived - the RRi time series (which is not a waveform yet!) is re-sampled in regularly-spaced temporal intervals (knowing the position of each beat allows this; and this time it is OK to assume the BPMs are known between the beats!)
- the frequency-transform (1/RRi) is computed
- either the RRi or frequency transform of the RRi is passed to custom_pwelch (which with one configured window computes the straight FFT result)
- the list of available frequencies is computed (in Hz)
- the total power density is computed
- for the two comfigured frequency ranges (
.hfreqand.lfreq), the sum of values (power density) is computed - if the relative power is requested, the ratio to the total power is computed
- as an additional measure the RMSSD (square root of mean of squared differences of successive heart-rate periods, i.e. the second discreet derivative of the onsets in seconds) is computed
- the results are stored in a struct
Usage example
For this example, we assume that the data was sampled at 500Hz and is stored in the third column of a text-based log file:
- computehrv_fullexample.m
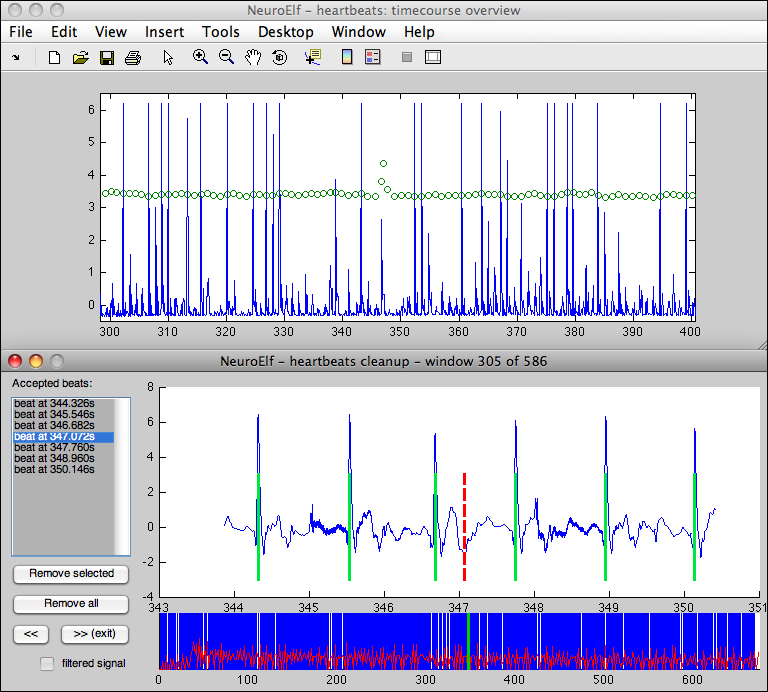
% read the data (use selector and change Filetype to .log!) ecg = xff('*.ntt'); % get the data in channel 3 ecg_data = ecg.ChannelData(3); % compute a transformation (to improve the detection of heartbeats) ecg_dt = abs(ztrans(ecg_data)) .^ 2; % run a first pass of detection and plot the result // options used are: % - freq: frequency (must be known for text-based files!) % - skewdt: since we squared (the absolute z-transform of) the signal, % we need to lower this value accordingly! % - detlength: with the squared transformation, peaks become very thin % spikes (<0.05 seconds!) % - plot: set to true to create outcome windows ecg_beats = heartbeats(ecg_dt, struct( ... 'freq', 500, ... 'skewdt', 0.05, ... 'detlength', 0.02, ... 'plot', true)); % re-run heartbeats with original signal and pre-detection // new options: % - bppre: used to pass in the already detected beats % - cleanup: show manual clean-up interface % - ecg_beats = heartbeats(ecg_data, struct( ... 'freq', 500, ... 'bppre', ecg_beats, ... 'cleanup', true, ... 'plot', true)); % pass beats to computehrv hrv = computehrv(ecg_beats, struct('freq', 500)); % plot periodogram plot(hrv.prawf, hrv.praw); % compute relative power contribution HFP/LFP rel_pow_HoverL = hrv.hfp / hrv.lfp;
The following screenshot was taken during this example (while the second call to heartbeats is being executed):
Note: if the function (heartbeats) is called twice with plotting enabled, the result of the overview of the first call will be re-positioned so that it can be easily used as input to the second pass.